内容摘要:本文提出了一种对双吊点水平臂架整体稳定性校核的计算方法,对其中横向弯矩和端弯矩及其载荷弯矩系数提出新的理解和求解方法,同时以具体实例为对象用Matlab软件进行了完整系统的分析计算,并与其它两种方法进行了对比,最后提出几点指导性建议。
关键词:起重臂,整体稳定性,横向弯矩,端弯矩,横向载荷弯矩系数
1、前言
稳定性是设计塔式起重机时应重点考虑的问题之一。近年来双吊点塔式起重机被广泛采用,但由于双吊点臂架是超静定结构,在实际计算中给工程技术人员带来很多麻烦。起重机设计规范(GB3811-83)与塔式起重机设计规范(GB/T 13752-92)对于这种型式的吊臂整体稳定性设计计算中的有关参数也未提供明确、充分的解释和计算方法。不少同行学者就这方面的问题曾进行过有益的探讨,但由于对臂架力学模型的简化处理和对各参数计算方法的不同,导致他们的结果存在较大的差异,给设计产品第一线的工程技术人员带来诸多不便与困惑。
本文首先就文献公式(31)中端弯矩Mo、横向弯矩M、横向载荷弯矩系数C等,在研读文献的基础上给出一种较为明确的解释和具体的计算方法,并以某种型号产品为例进行了具体计算。此外,本文按多数学者认同的一种方法,即在考虑横向载荷引起的横向弯矩时,将吊点处按简支处理(以下简称“简支法”)进行了计算,并将两种结果作了比较和探讨。
在校核臂架的整体稳定性时,除按本文提出的方法及上述提到简支法外,还按另外一种方法进行了校核,即公式(31)中CoxMox+CH用所考虑校核段内截面弯矩最大值代替。回转平面内计算类似考虑(以下简称“最大弯矩法”)。这种方法在校核跨外吊重工况(比如工况5)时,文献曾经使用过。最后本文将三种方法的校核结果做了对比分析。
2、起重臂结构型式及尺寸参数
本起重机的起重臂为小车变幅水平臂,结构型式为变横截面的三角形格构式构件,支承方式是臂根为铰支,带双拉杆的双跨外伸梁。起重机上下弦杆为等边角钢焊接拼方,斜桁架(斜、直)腹杆及水平桁架斜腹杆为无缝圆钢管,水平桁架直腹杆为等边角钢,两拉杆为实心圆钢。
2.1结构简图
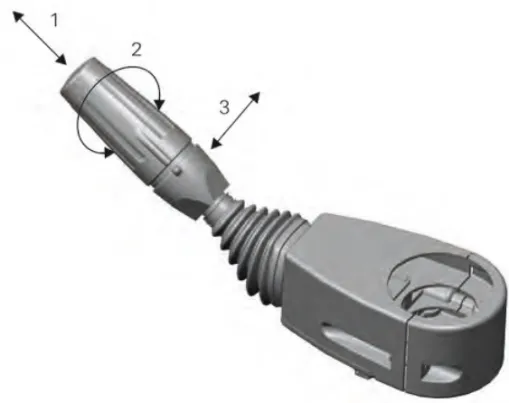
该臂架结构如图1所示,共分四个不同截面段。两拉杆长度分别为L=16971mm,L=49222.1mm。
2.2载荷参数
臂架每节段平均重力密度、风载与惯性载荷合成的载荷密度如下表1所示,其中风载与惯性载荷合成的载荷密度由文献中规定的方法求得。
2.3截面特性
该臂架各截面均为三角形,上下弦杆由等边角钢拼方焊接而成,截面简图如下图2所示,其中各截面参数如表2所示,截面两方向的中性轴分别为x-x,y-y。

2.4考虑的工况
本文共考虑了五种工况进行计算,各工况下吊重的位置及其计算载荷如表3所示。其中,起升平面Q由公式Q=(Qφ+q)φ+G求得,式中Q为额定吊重,φ为超载系数,φ为动载系数,q为吊具及50%起升钢丝绳重量,G为小车及50%起升钢丝绳重量;回转平面Q为吊重所受风载及惯性载荷的合成,其值由文献中规定的计算方法求得。

3、起重臂弯矩及其挠曲变形计算
塔式起重机的工作状况包括起升与回转两个平面。计算分析吊重在各工况下整体稳定性的关键是求解臂架的弯矩和挠曲变形。
在起升平面内,双吊点起重臂为一次超静定结构,它由臂架及两根拉杆组成,根据叠加原理,可分别计算单独载荷(包括OA、AB、BC段臂架自重、变幅机构、各工况等)作用时在各构件上产生的内力和变形,然后将所有内力和变形分别叠加,即得到所有载荷共同作用在各构件上产生的总内力和总变形。对双吊点起重臂这一超静定结构,可用力法方程来求解,即将作支承用的一根拉杆(比如内拉杆)切断并代之以多余约束力得到静定结构。其中,在计算力法方程中的柔度系数和自由项而采用图乘法进行积分时,对于臂架只计及弯矩对位移的影响,对于拉杆只计及轴力对位移的影响。求出吊臂弯矩以后,如同求解基本结构位移一样,可求出相应载荷下吊臂任意截面处的挠曲变形。在回转平面中,吊臂可视为悬臂梁,因此为静定结构,其内力和变形比较容易计算。
4、稳定性公式中几个参数的理解和计算方法
文献2公式(31)中涉及到弯矩M,M,M,M,及相应系数C,C,C,C。本节将给出具体的解释和计算方法。
4.1 M:以OA段为考虑对象在进行整体稳定性校核时,本文认为M指起升平面内作用于OA段内横向载荷在OA段上所产生的弯矩绝对值最大者。如考虑工况2并用OA段校核时,则应考虑OA段臂架自重(为均布力)、变幅机构自重(为集中力)、工况2吊重(为集中力)三种段内横向力在OA段内各自产生的弯矩绝对值最大者,分别记为M,M,M。
4.2 C:关于相应系数C,C,C的计算,需先求出在各自载荷作用下OA段上产生的最大位移△,△,△,再根据文献2附录I即可求得C,C,C。最后按公式∑CM=CM+CM+CM求和合成。
4.3 M:在所考虑的各种载荷作用下,起升平面内OA













































































































































热门推荐